When Models Give Different Answers To The Same Question
Incorporating Non-Deterministic Tools Into Deterministic Processes
In the world of machine learning and artificial intelligence, we characterize models as either deterministic or non-deterministic. Deterministic models, like a regression model or a random forest, always produce the same output for a given input. Non-deterministic models – which include large language models (LLMs) like GPT-4o or Claude-3.5 – can produce different outputs when given the same input multiple times.*
This post focuses on a specific challenge: how to use a non-deterministic model as part of a larger deterministic process. We’ll explore this in the context of binary classification problems – tasks where each observation needs to be sorted into one of two possible buckets, like “pass” or “fail.” Examples include screening resumes, adjudicating insurance claims, or determining if something is cake or not cake. We focus on binary classification because it’s the simplest type of model. And for generative tasks – like answering questions – some of the same principles apply, although there’s an additional set of problems associated with processing the output data (the text).
The Importance of Determinism
When we use AI models to help with classification tasks (or any kind of tasks), we want to know what the model is doing. For example, if asked whether our process would reject a particular resume, we want to know the answer and have that answer be consistent. This is important for our own understanding of what our tools are doing, as well as for building user trust.
What about getting valid accuracy numbers? Do we need determinism for that?
With a non-deterministic model, the accuracy for any single observation can vary. Some predictions will be lucky (correct), while others will be unlucky (incorrect). However, when we look at the model's performance across many observations, these individual variations tend to average out. The larger the sample, the more stable and consistent the overall accuracy numbers are likely to be.
We can further characterize accuracy by performing multiple runs and expressing model performance as a range of accuracies observed across these runs. For example, we might find that our model's accuracy typically falls between 85% and 92% for our sample data.
Because of this, we can get consistent accuracy statistics for a model, even if it’s not deterministic.
Each Response Is an Independent Sample from a Distribution
When you query a non-deterministic language model, you’re sampling from a distribution. This distribution will depend on your input and your model.
For instance, if your question is “Who was the first president of the United States?” and your model is GPT-4o, every response will include the name “George Washington.” If you ask it to pick a number between 1 and 100, the responses will have numbers, but not a uniform distribution of numbers. (Some are more likely to be returned than others, because it’s not actually doing random number generation).
If you have your model solve a classification problem and limit the responses to just 0/1 or pass/fail, then for each prompt (like a resume or an insurance claim), the population you’re sampling from is just a combination of passes and fails, in different proportions for different prompts. But the process is the same: each time you prompt, you’re sampling, and each prompt is an independent sample. This fact can provide us with some intuition and strategies.

Strategies for Incorporating Non-Deterministic Models
If we use the model once for each input and take that as our decision, we may get random variability: that’s the lack of determinism. But we can mitigate this risk via the following:
Repeated sampling: We pass each input to the model multiple times. The number of times might be the same for each input, or it might be based on the value of the outputs. (We might even stop sampling after the first output if we get a certain value.)
A decision rule based on the outputs: We might take the modal (most common) value. We might take the minimum output value or the maximum value. (In a binary classification context, taking the minimum means that if 0 is ever output, we use 0, and taking the maximum means that if 1 is ever output, we take 1.) Or we might check with a human if the model is giving certain types of outputs – for instance, if the outputs are mixed, or mixed in certain ways.
We can develop a specific strategy for both of these steps based on simulating different strategies and thinking through the trade-offs for our specific problem.
Trade-Offs to Consider
Here are some of the trade-offs to consider in implementing your strategy:
Accuracy: We can have a totally deterministic model if we sacrifice accuracy – we can always pass or always fail – but it’s not very useful.
Compute Costs/Time: If there is any signal in the noise – if the underlying population we’re sampling for any given input has more of the true value than the false value – then we can get to the correct label for that given input just by continuing to sample, but we might be sampling more than is worth it.
Human Input: If humans can label the inputs correctly, we can have a totally accurate, totally deterministic model by just having people do it instead of our machine learning model – but presumably, there was a reason why we didn’t do that in the first place.
Simulating Different Strategies
How do you determine which decision rules to adopt? Do you sample three times or five? Do you stop when you see three in a row of the same output value? Do you use the mode, min, or max? Under what circumstances do you send this to a person to review?
I highly recommend starting with some labeled data and your prompt, sampling to get outputs from the model you’re using, and then simulating various decision rules to see what gets you the best results, given your personal accuracy/compute/level of human input trade-offs. If you’re worried about “overfitting” your decision rule, split your data, “fit” your decision rule on part of it, and then try it out on the data you didn’t fit it based on.
Instead of relying solely on simulation, is there a way to use a smaller number of samples to estimate the underlying distributions of the populations we're sampling from, and determine strategies from that? I briefly considered this hybrid sampling-inference method for a different problem and I couldn’t figure out how to do it. But there may be statistical techniques that could effectively combine limited sampling with distribution estimation, potentially offering insights with less computational overhead.
Something else to keep in mind: the distribution you get back from one of these models for any given observation is not a statistical measure of uncertainty in the same way that it would be if you trained a model for your specific task. An observation that returns “fail” 10% of the time isn’t necessarily less likely to represent a true failure than one that returns “fail” 30% of the time. These results might actually relate to the true labels, but there’s no way to know without testing.
Example Model and Simulation
I set up a toy example with the following attributes to test the impact of the number of times we sample and how we determine what value to use on several metrics:
We have a labeled data set with 95% “zero”s and 5% “one”s
There’s a 5% chance, for both the true positives and true negatives, the model gets the answer wrong. This is random.
We’re just varying the number of times we sample for each observation, and in the simplest way possible – we’re not basing it on any specific pattern, we’re just taking the same number of samples for each observation
We’re then taking the mode of the responses, and that’s our final process output
This is the simplest possible type of model because the error probability is the same for each observation. It’s also the simplest way to evaluate decision rules, since we’re taking the same number of samples for each observation, not having additional stopping criteria based on the values we’re seeing.
What am I looking for here? I’m looking for three attributes:
The accuracy rate: How accurately does our process label our data?
The consistency rate: For instance, I run the simulation once, then run it 999 more times and see what proportion of these simulations are in agreement with the first run’s results. (For more sophisticated ways of measuring consistency, this is a good rundown of inter-rater reliability metrics.)
The average of samples we have to pull, or how computationally intensive this is: In this case, this is just the number of times we sample for each observation, because we’re not stopping early based on the results.
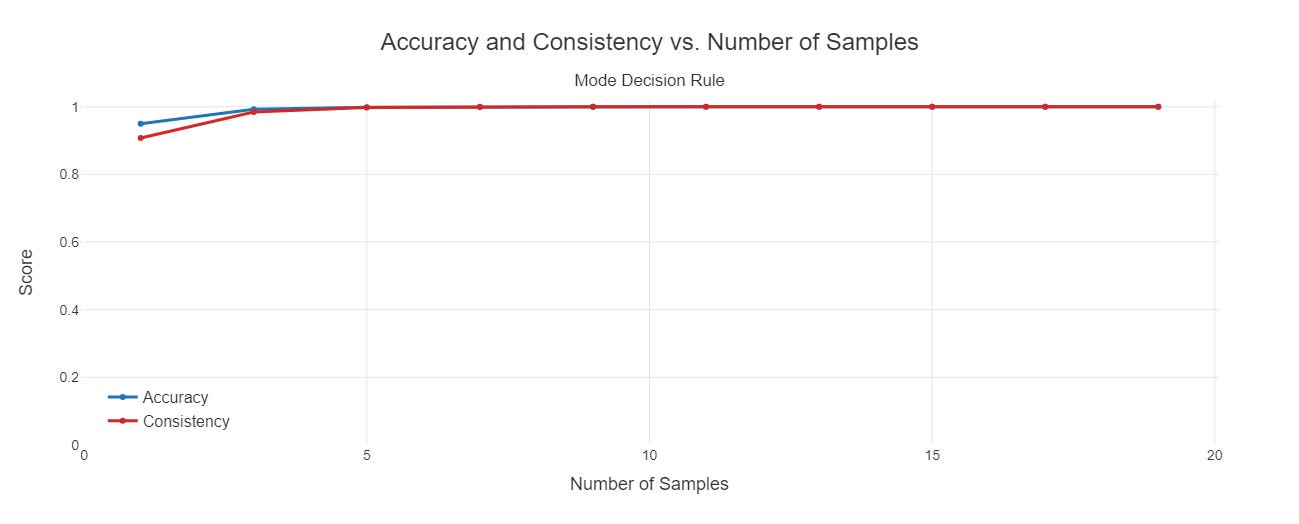
You can see below that accuracy and consistency both increase as a function of the number of samples.
Here are the statistics describing the values at 1 and 19:
Accuracy with 1 sample: 0.9501
Accuracy with 19 samples: 1.0000
Consistency with 1 sample: 0.9078
Consistency with 19 samples: 1.0000
Average number of samples (min): 1
Average number of samples (max): 19
However, it’s not a given that we’ll see these two lines either moving up or moving in concert with each other: we’re seeing this because of our specific decision rules in combination with how we built the model.
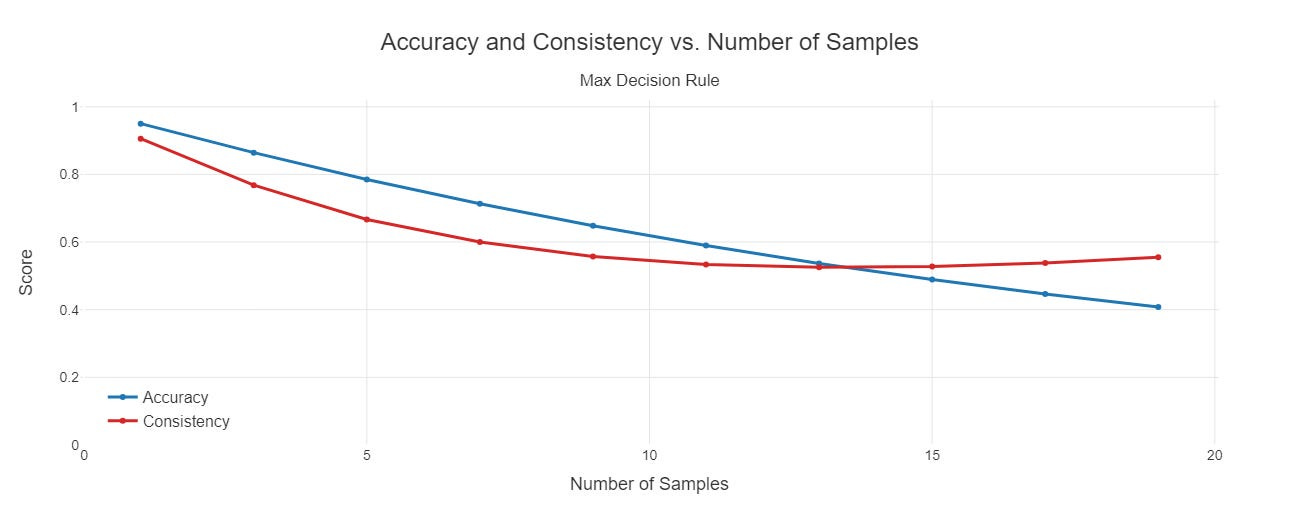
For instance, in this example, if we take the max instead of the mode as our value, both lines initially decrease as the number of samples rise and we incorrectly label more values 1. But there’s inconsistency in terms of which values these are across each simulation, since this is totally random. This is why we also see the consistency line decreasing as a function of the number of samples, but then starting to increase as we start falsely labeling most of the observations! If we were to keep going, consistency would approach 1 and accuracy would approach .05, or the proportion of true positives.
Conclusion
Using non-deterministic models shouldn’t scare us: to the extent that we need determinism, we need it in our overall process, not in any single component of that process.
What’s more, various alternative processes also might not be deterministic. For instance, a resume-screening process involving people may be non-deterministic because different people who review resumes make different decisions, or even because the same person makes different decisions based on mood, time of day, or what resumes they’ve looked at prior to a given resume.
Non-deterministic ML models, as opposed to non-deterministic people models, come with significant advantages thanks to how easy and cheap it is to run these kinds of simulations. And the implementation isn’t that different from a deterministic model: we’re just periodically retesting and validating the whole process, including our sampling and decision rules.
Are there scenarios where the lack of determinism should be an absolute dealbreaker? Not necessarily. Sometimes the model itself simply won’t be good enough to use. But, at least in the case of a binary classification model, if you run it once and get accuracy numbers you’re comfortable with, I think your distribution would need to have some really weird properties or you would have to have gotten extremely lucky on that first pull for you to not be able to repeatedly sample, experiment with different decision rules, and get to a combination of both a very high level of consistency and at least as good accuracy numbers as you got that first time. But that’s just a hunch; I haven’t tried to model this with every possible kind of distribution.
______
*There’s ongoing discussion about what drives this behavior and whether these models are truly non-deterministic or if users simply lack control over the criteria that would make the model act deterministically. For the purposes of this discussion, that distinction isn’t relevant.