Validating What, Exactly?
Will My Model Generalize?
When we’re using models to generate labels or predictions, like in the context of machine learning, we often want to validate those models to quantify their performance. But what does 'validation' mean? How is it different when we’re using a model we’ve trained ourselves, vs. more of a heuristic (“Does the text contain a certain word?”), or when we’re having an LLM that we haven’t trained for a specific task do our classification for us?
Let's start with a contrived example.
Imagine we need to separate two different kinds of texts: pasta recipes and instructions for making bombs. Among a million pasta recipes, there are a few bomb recipes, and our task is to correctly identify all of them by dawn. It’s like Cinderella, except we’re separating different kinds of text instead of picking the peas from the ashes. And there are no tricks here: everything is in English, there are no weird formatting issues, and none of the texts have been modified to be semantically similar but use different words.
This is a binary classification problem with two categories: pasta recipes and bomb instructions. Each piece of text belongs to one and only one category. How do we solve this? We have multiple options.
We could flag every text with the word ‘bomb’ in it.
We could use semantic similarity and flag all the texts that aren’t within a certain semantic distance of at least one of a hundred random pasta recipes.
We could train a text classification model like BERT on a sample of pasta recipes and a sample of random unrelated texts. BERT is a language model that, like the OpenAI models, is based on the transformer architecture. By giving it pasta recipes and other texts and labeling each, it will learn the features of pasta recipes and how to label new texts as whether or not they belong to that group.
We could even use an LLM like GPT-3.5 or GPT-4 for classification by asking it, “Hey, is this a pasta recipe or a set of bomb-building instructions?”, though it might be overkill in terms of time and expense. This would be an example of an ‘LLM-led evaluation,’ or using an LLM as an ‘autograder.’
Assuming we’ve chosen one of these methods, we now have a ‘model’ that takes inputs and makes predictions. To validate our model, we can compare its classifications against labels created by humans. No matter which method we selected, it's likely to perform well, with high recall (correctly identifying all bomb instructions as such). And if it doesn’t have super high precision (that is, if we occasionally catch pasta recipes which somehow manage to have the word ‘bomb’ in them), that’s fine; we can manually filter those out.
But have we truly validated a model for identifying bomb-building instructions? Sort of, but what we've really validated is a model for identifying bomb instructions among pasta recipes, where both are formatted in a particular way. The model's performance is specific to this particular context, with ‘cleanly separating’ types of text data.
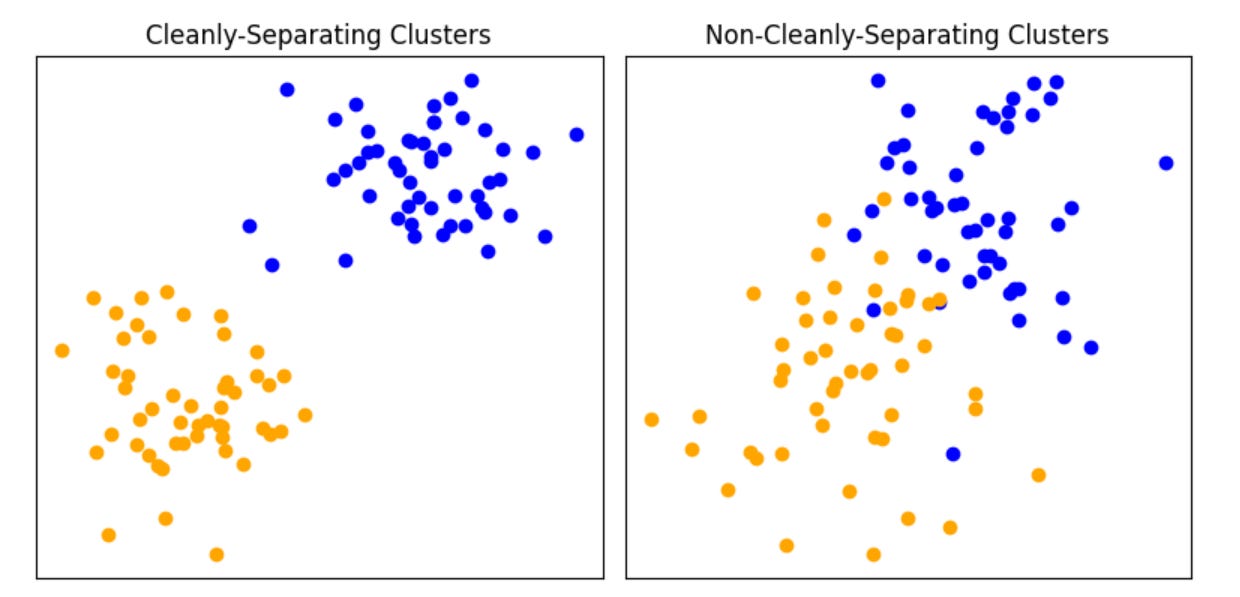
Now, consider a more challenging scenario. We’re again given two sets of texts, pasta and bombs, but some instructions are in other languages, rephrased to avoid words like ‘bomb,’ have random spaces inserted, or use ASCII art. Our previously validated model might struggle with this new data set. This illustrates the issue of generalizability: a model that performs well on one data set might not perform well on another with different characteristics. When we talk about ‘validating’ a model, what we’re really talking about is validating the combination of the model and the data.
In this discussion, it's important to note that we're using the term ‘model’ in two distinct senses. On one hand, we have formal statistical models, which are trained on data and provide probability scores expressing certainty. These models are typically used in machine learning and involve algorithms that can learn from and make predictions on data. On the other hand, we're also referring to more heuristic approaches as ‘models’ – for instance, rules like "flag all texts containing the word 'bomb," or even LLMs that are doing tasks that we have not specifically trained them to do.
These aren't formal models in the statistical sense, but they’re still tools that make predictions. When we talk about validation and generalization, we're applying these concepts to both formal models and heuristic approaches, even though their underlying mechanisms and the ways we assess their performance may differ. And when we use LLMs to perform classification on tasks they haven't specifically been fine-tuned on, like when we ask, “Is this a recipe for pasta or a set of instructions for how to make a bomb?”, what we’re doing is closer to a heuristic approach than a formal statistical model for the purposes of validation. Which doesn’t mean it might not be extremely accurate: you can have very accurate heuristic approaches and not-very-accurate formal statistical models.
Imbalanced Data Sets and Validation Challenges
One challenge in validating models as in our pasta/bomb example is dealing with imbalanced data sets. In these cases, the rarity of one class (e.g., bomb instructions among pasta recipes) means that if we select texts to label via a random pull, this is likely to miss the critical minority class entirely. This imbalance poses a problem because our model absolutely needs to be able to correctly identify the rare class, but it's difficult to validate this ability without sufficient representation in the labeled data.
To address this, we might consider targeted labeling strategies, where we specifically seek out examples of the minority class to ensure they’re adequately represented in our validation set.
Quantifying Uncertainty in Trained Models
When we train a model, like fine-tuning BERT on labeled texts (pasta vs. not-pasta, or pasta vs. bomb), we can obtain probability scores that express the model's certainty. These scores allow us to adjust our classification threshold or decision boundary differently for new data sets. On really cleanly separating, bimodal data, it doesn’t matter where we draw the line – but on datasets where there are data points in the middle, we need to think about how to classify those middle points, and draw that decision boundary accordingly. For instance, if we were classifying pasta vs. not-pasta among a general data set of recipes via our initial pasta vs. not-pasta BERT model, we would likely get some in-the-middle scores for other food recipes, especially those with some ingredients that are typically found in pasta recipes.
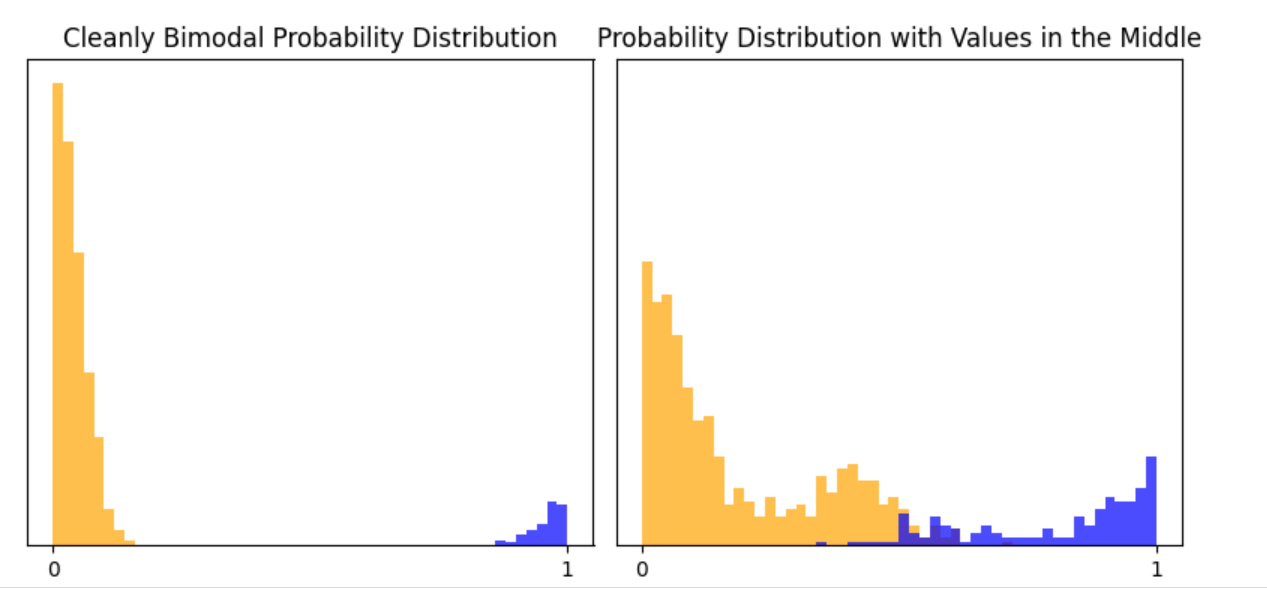
Additionally, if we want to update our model for new data, we can focus on labeling data points where the initial model was most uncertain. This strategic labeling can improve model performance with less effort than randomly labeling new data. And we have a framework for how to update our model – label some data points and retrain – unlike if our heuristic was simply searching for ‘bomb,’ where we have to find some brand-new heuristics.
Quantifying Uncertainty in Heuristics or LLM Evals
But when we haven't trained a model but instead have used a heuristic approach (like searching for the word ‘bomb’), we don't have probability scores. The same concept applies to LLM-led evaluations, where an LLM performs our classification task even though it hasn’t been specifically trained to perform it. This includes the use of rubrics like the following, which we can use to get LLMs to assess either text people have written or synthetic data from other LLMs. We give this rubric to an LLM, along with some text, and it returns either a PASS or a FAIL.
class GradingPipetteCleaningInstructions(Enum):
PASS = """Includes instructions for all of the following tasks:
using distilled water, use of mild detergent or cleaning solution,
rinsing with distilled water, drying, reassembly, wearing gloves and
goggles, checking for calibration and wear"""
FAIL = """Leaves out one or more of the following tasks: using distilled
water, use of mild detergent or cleaning solution,
rinsing with distilled water, drying, reassembly,
wearing gloves and goggles, checking for calibration and wear"""To see if the model generalizes to new data – like that from new LLMs – we need to label some data from the new population and compare the model's predictions. We might do that randomly. We might use probability scores (or logprobs) from the LLM about its degree of confidence – which aren’t the same as if you’d actually trained a model on your data, but they still could be useful measures of uncertainty.
At What Point Do We Say, ‘This Generalizes Generally’?
But then, when can we say, “Hey, this thing generalizes across new data? We’ve sufficiently validated this”? Let's say we have a model that we’re using to grade essays. We made a heuristic based on one class and then it worked great on six other randomly selected sections. Do we feel good that it’ll work on next semester’s essays?
Not really, no. I’d probably say, “You still need to keep labeling data.” There might be something different about next semester’s essays.
What about with new LLMs? Let’s say I’m using LLM evals to benchmark LLM performance on a particular set of tasks. Or I’m using them to flag output as “dangerous” – like, “It explained how to make bioweapons!” At what point am I confident that a new LLM is going to have content that’s structured sufficiently like content we’ve seen before, such that I no longer need to manually label new content and assess?
I have no idea. The best I have, in practice, will look something like “I formulated a rubric based on data from five LLMs. I tried it on four more LLMs and it totally worked! I feel like we’re good on this.”
Or alternatively, there are areas where a grader has worked so well on such weird edge cases that I’d feel good about using this on new data. For instance, in named entity recognition, GPT-4 identified that “Lynux” (a misspelling of Linux) was a software tool or programming language, presumably based on either the context (being in a list of software) or the syntactic similarity. That seemed to me like an indication of robustness. We could also generate other types of edge cases and evaluate performance on those.

But if I were a statistician trying to quantify confidence level, I’d want something more than that.
Models With Less Validation Are Everywhere
It's important to note that not every model needs formal validation. We often solve classification problems without validated models. When you ask someone a question in a job interview to determine if they should get to the next stage, you’re engaging in binary classification, and you probably never did any predictive validation to make sure that people who perform better on your questions also perform better at the job you’re hiring for. (And are other kinds of validity checks as well, like whether what you’re asking measure the concept that it’s intended to measure.)
Formal validation on a specific data set without generalization can be useful, too. If you're dealing with a large amount of data from the same population, a model that works well on that data set is sufficient. In the case of LLM evals, a model that performs well on one LLM could be useful if you want to analyze sensitivity to how a question is phrased, or even just what percentage of time the model gets the question correct.
Mitigating Risk With LLM Classifiers and New Models
When we talk about validation and model type, it’s worth really thinking about your use case. What are you trying to do? How good does it need to be before it’s worth using? If it’s going to break, how might it break, and how are you going to monitor for that?
Saying that we’re going to keep selectively labeling and monitoring – in other words, that we’re never confident that it’s going to keep generalizing to new populations – is never a bad answer.
But what if that’s not feasible? Like, we want benchmarks that will autograde output from new LLMs. We have time limitations, a million different autograders for evaluations of different prompts, and a whole lot of text, so we can’t validate each model on each new LLM. We still have a few tools we can use (and, ideally, test out ahead of time):
Multiple filters for each text: for instance, looking for keywords in addition to using autograders
Using the logprobs as model uncertainty measures by which to flag outputs for human review
Evaluating a few autograders on each new model, even if we can’t evaluate all of them. This could involve tests of knowledge we know each model has, to make sure that it’s appropriately flagged
Anomaly detection, out-of-distribution detection, or other methods of evaluating whether the new population looks the same as the data that was used to test
Also, to revisit the issue of validation in extremely imbalanced situations, how do we validate a model to see whether it can detect capabilities that don’t yet exist among any LLMs? For instance, how do we validate that it can correctly detect if the model explained how to weaponize anthrax (or whatever) if no model can currently explain this?
We have to come up with ways to generate data that parallel as closely as possible what we’ll be doing in our tests. For instance, we can give existing LLMs varying degrees of hints or information in the prompts. But if you’re asking about things you don’t want the LLM to learn about, use a way of interacting with LLMs you’re sure won’t get used to train the next LLM!
There are good solutions available here, even if we can’t necessarily quantify uncertainty about whether our models will generalize to populations they haven’t seen before.


Very well written! I appreciate the time you took to properly communicate the problem set and some possible solutions.