How Many Dice Rolls Does It Take to Pick Two Non-Cursed Arrows?
I got nerd-sniped by an XKCD comic.
In it, the player randomly grabs 2 arrows from a group of 10, 5 of which are cursed (yikes!).
The Dungeon Master (DM) has them simulate the chances of avoiding the cursed arrows by rolling some dice: specifically, three six-sided dice (3d6, as we say) plus one four-sided die (a d4). If the sum of the dice is 16 or higher, the player managed to grab only non-cursed arrows. Success!
But why those specific dice? I like to think I have some intuition about probability distributions, but I had zero clue why the way to simulate this problem was that particular set of dice rolls. But I really wanted to know.
What Are We Actually Solving Here?
Let's work through this step by step. When you reach into that quiver:
You could grab two cursed arrows (bad luck!)
You could grab one cursed and one regular arrow (still failed!)
Or you could grab two regular arrows (jackpot!)
We want to know: What's the chance of the jackpot scenario? And then, how do we simulate that chance using standard D&D dice?
Following the Arrows
You might think since half the arrows are cursed, you have a 50-50 chance each time. But it's not quite that simple because you're grabbing two arrows, and you're sampling without replacement – you don't put the first arrow back after you pick it.
On our first draw, there's a 1/2 chance of grabbing a safe arrow, in which case we proceed to "NC" (non-cursed). If we get that lucky first draw, we then have a 4/9 chance of grabbing another safe arrow on our second draw, because there are 9 arrows left and 4 are non-cursed. If we hit both of these, we've succeeded, and we wind up at the green dot on top, for 0C (0 cursed).
This is actually a perfect example of what's called a hypergeometric distribution – what we use when we're sampling without replacement from a finite population (in this case, 10). Unlike a binomial distribution (like coin flips), the probability changes after each draw because we're not putting items back. The hypergeometric distribution is particularly common in quality control (sampling from a batch of products) and card games (drawing from a deck).
Following the tree by multiplying out the probabilities, we find the chance of zero cursed arrows is 1/2 × 4/9 = 2/9, or about 22%. That's what we're going to be trying to simulate – we need a set of dice rolls where we can pick a number (a cutoff score) and have a 22% chance of rolling that score or higher.
Also, while it doesn't matter for this problem, this also shows us the probability of getting one cursed arrow is 5/18 + 5/18 (the probability of 1 non-cursed + 1 cursed, plus the probability of getting 1 cursed + 1 non-cursed), or 5/9. And the probability of getting two cursed arrows is 2/9, or the same as getting zero cursed arrows. Which makes sense, because we started with half of the arrows being cursed.
You can see each of those probabilities in the bar graph below:
And for the mathematically curious, the probability formula is:
where:
k is the number of cursed arrows drawn, n is the total arrows drawn, and C(a,b) is the combination formula:
The Tricky Part: Finding the Right Dice
How do we roll dice and set a cutoff that corresponds to a 2/9 probability? If we just had a nine-sided die, this would be easy to simulate: roll the d9, an 8 or 9 means you pass, anything lower means you fail.
But even the best DMs don’t have a d9.
Instead, if you’re playing a game involving extensive dice rolls, you probably have dice with 4, 6, 10, 12, and 20 sides.
I was hoping to find an analytical solution – to solve an equation – to get to the 3d6 + d4 solution. I didn't get there. But I did write code that simulated different combinations of dice, and it got to 3d6 + d4, and I'll show you how to check that result and find the cutoff score.
I also found another method where I think the intuition might be a little easier, both for solving for what dice to roll and finding the cutoff score: where instead of adding the dice results, we multiply.
The Addition Method
The initial problem setup – where we use the 3d6 and the d4 – involves adding the results. Let's look at how that plays out.
This is the probability distribution for the 3d6 + d4 roll. The lowest score you might get is a 4, if the dice all come up 1s. The highest score you can get is a 22, if you get a 6 + 6 + 6 + 4. The scores are symmetrical around the median, which is at (4+22)/2 = 13.
In order to find the cutoff score, we start from the bottom and keep adding the height of the bars until we get to 1 - 2/9, or .78, which happens at 15. (The other way of saying this is that the integral of the probability distribution from 0 to 15 equals 7/9, and therefore rolling a 16 or higher gives us our desired 2/9 probability of success.)
But working backwards – starting with "I need a 2/9 chance" and figuring out which dice to use – that's much harder. There's no obvious way to look at 2/9 and know you should roll 3d6 + d4, and because there are so many different possible dice rolls with four dice, you've also got to do a bit of math to come up with the distribution.
So it got me wondering if there was a more intuitive way to generate a distribution that also has a 2/9 cut-off. And there kind of is, sometimes.
The Multiplication Method
What if instead of rolling dice and adding the result, we were to multiply? We're still aiming for that same 2/9 probability of success, but we'll try to get there a different way.
To start with, we're going to need a combination of dice where, when we multiply them together, the number of possible outcomes is divisible by 9 (since we need exactly 2/9 of all possible outcomes to be successes).
Let's look at our dice again: we have 4, 6, 10, 12, and 20-sided dice. Just from eyeballing that, the simplest way to roll a set of dice that get us to a multiple of 9 is to roll 2d6. That gets us 6 x 6 possible outcomes (although they’re not unique – some repeat – which we’ll get to later). You can see that the results go from (1, 1) = 1 to (6,6) = 36.
The chart below represents all of the possible outcomes. The number across the top represents the outcome of the first roll, the ones on the side the second roll. The numbers in the middle show the results from multiplication.
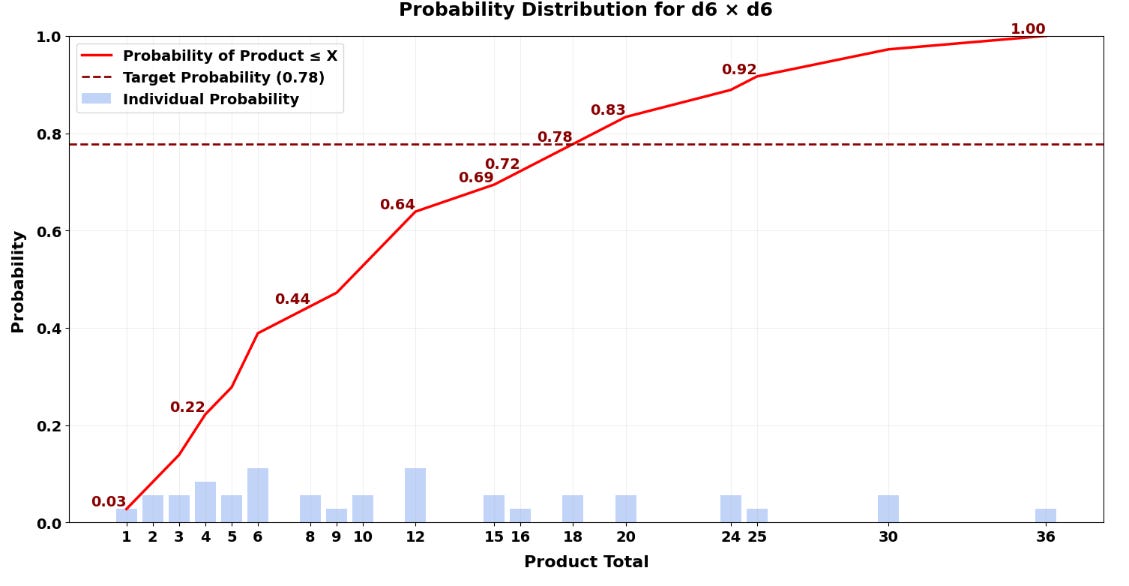
And, unlike with the addition method, because there are only two dice here, you can actually find the cutoff manually. How? Well, there are 36 possible (non-unique) outcomes. 2/9 = 8/36, so pick the top 8, and there's your cutoff. I did it by color-coding the top 8 in yellow.
You can see that, by rolling two d6s, multiplying them, and setting a cutoff score of 20, you can also simulate the 2/9 probability that you need – and because there are fewer dice, it’s a bit more intuitive.
The bar graph below shows those same numbers but as a probability distribution instead.
But, Actually...
This made me wonder: Could we use this multiplication approach more generally? Would any set of dice work to simulate this, so long as the total number of possible outcomes is divisible by 9?
Nope!
Let's look at d12 × d12 = 144 outcomes. It's divisible by 9. If we could set a cutoff that would get us 2/9 x 144, or the top 32 possible outcomes, that would give us 2/9.
But here's where probability distributions get really interesting: when you actually map out all possible rolls, there's no cutoff point that gives exactly that many outcomes. This is because multiplication creates what mathematicians call a non-uniform discrete distribution. When we multiply numbers (or add them), some products appear more frequently than others (like how in our 2d6 table, 12 appears in multiple cells), creating clusters that make it impossible to cleanly slice off exactly 2/9 of the outcomes.
The 2d6 case working so perfectly (with exactly 8 results of 20 or higher out of 36 possibilities) turns out to be more about luck in how the numbers cluster than any mathematical property we could have predicted in advance.
But it is the case that, because of how multiplying numbers results in more unique results than adding them, you can cluster more granularly. Because of this, I suspect you’re somewhat more likely to be able to get to any given probability with fewer dice rolls. This would make it a little more intuitive and less math-heavy than the additive way.
That Was Mildly Interesting!
I was hoping to find a neat mathematical formula for how to get to 3d6 + d4, and I was a little disappointed that I didn't. But the nice thing is that simulating this sort of thing is really easy in Python. You can see my code here.
Probability distributions are really interesting. Of course, most of the time, in real life, you're working backwards from the data – the results of your draws from the population – to try to find the probability distribution, rather than calculating your sample based on the distribution!
So I'll leave you with another piece of math: If you draw two arrows, but you don't know how many cursed arrows there were, what can your results tell you about how many cursed arrows were in the quiver to begin with?
This is where Bayesian inference comes in: it lets us update our beliefs based on new evidence. If we start with no prior knowledge (equal probability of 0-10 cursed arrows) and draw two arrows:
If both are cursed: We'd expect about 8 cursed arrows total
If both are safe: We'd expect only about 2 cursed arrows total
If we draw one of each: Our expected value is exactly 5 cursed arrows
Which just goes to show – even a small sample can tell you something meaningful about the underlying distribution, if you're starting from very little knowledge.
But How Many Dice Rolls Does It Take?
After all this probability analysis, we can finally answer the title question properly:
If you're adding dice (like our original 3d6 + d4 solution), you need 4 dice to simulate picking up some arrows.
The multiplication method with 2d6 gets us there with half as many dice, though it's not how D&D typically handles probability.
But here's the actual answer: you can get it down even lower than that. You can roll an average of 1.11 dice if you just use a d10, count 8-9 as success, and reroll on 10s.
And if you have a d100 sitting around, you can get it down even further, but that is left as an exercise for the reader.